I'm talking about "real" again. This class is abstraction built upon abstraction in the form of the theory needed to bring rigor to the underpinnings of the calculus.
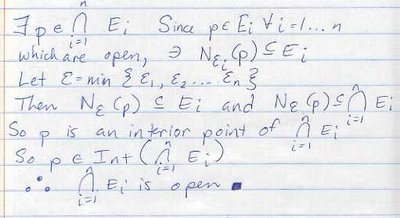Does anyone reading this see the above notes as concrete?The reason I titled this post "reality check" is because the author of this textbook needs a "real"ity check. Here is a sentence from the text that made me laugh out loud:
"A thorough understanding of these topics on the real line will prove invaluable when they are encountered in MORE ABSTRACT SETTINGS."
Um . . . if this isn't abstract, what is it?!
And to think my algebra students ask me where they are going to use ALGEBRA in REAL LIFE!
PS Antonio, the last time I posted about "real" you asked why I only included a "sentence" rather than a "paragraph." Here's your paragraph, and here's a little pop quiz to keep you sharp. What does the "paragraph" here prove?
2 comments:
I'm with you Heidi - after they finally get good at algebra, then the students might get the joy of taking Abstract Algebra! Now that's funky stuff.
Your posting brings back old memories! (Not necessarily fun ones!) But I can rise to your challenge, I believe. Without the statement at the top it's a little unclear. However, I think it's saying that if the intersection of a collection of n open sets is non-empty, then that intersection is an open set.
Brian
Yes . . . I just got on to add that it needs to be a FINITE union of open sets in order to be open, but I notice you covered that by saying "n."
Yeah, anyone who has not taken Abstract Algebra has no means of imagining anything with "algebra" in its title being SUCH an entirely different world from the algebras taught at the high school level. It seems, by the name, it should be the next step up. The reality is that it is a leap over the Empire State Building to go from one to the other!!
Post a Comment